弦图：从入门到入入门

弦图：从入门到入入门

lzqy_

·

2022-04-13 20:56:09

·

算法·理论

总结了一下网上现有的零散弦图资料，并补充了部分证明。

由于笔者实力有限，若文中有任何问题，望指出！

目录

前置定义

引理

最大势算法（\text{MCS} 算法）

应用

弦图判定

弦图染色问题/最大团问题

弦图最小团覆盖/最大独立集

区间图

前置定义

基础定义：

完全图：对于任意的点 u,v∈V，有 \{u\rightarrow v\}∈E。

弦：连接环上不相邻两个点的边。

子图：点集为原图点集子集，边集为原图边集子集。

导出子图：点集为原图点集子集，边集为所有满足 两个端点均在选定点集中 的图。

团：完全子图（显然一定是导出子图）。

点割集：若点集 V 是 u,v 的点割集，则在原图中删除 V 的导出子图后，u,v 不连通。

极小点割集：若点集 V 是 u,v 的极小点割集，不存在 u,v 的点割集 V' 满足 V'\subsetneqq V。

最大团：点数最多的团。

极大团：若点集 V 的导出子图是极大团，则不存在点集 V' 的导出子图是团，且 V\subsetneqq V'。

红色部分是原图的子图、导出子图、团、最大团、极大团。

弦图：任意大于 3 的环都有弦的无向图。

左图是弦图而右图不是。因为右图存在一个 \{1 \rightarrow 2 \rightarrow 3 \rightarrow 4 \rightarrow 1\} 的长度为 4 的环，且没有弦。

为解决弦图问题引入的定义：

单纯点：设与点 x 相连的点集为 N(x)，若 x 为单纯点，则点集 V=\{x\}+N(x) 的导出子图是一个团。

完美消除序列：令 n=|V|，完美消除序列为一个 n 的排列 \{v_1,v_2,\dots,v_n\}，满足 v_i 在点集 V=\{v_i,v_{i+1},\dots,v_n\} 的导出子图中是单纯点。

上述弦图存在一个完美消除序列 \{4,2,1,3,5\}，单纯点有 1,4,5。

引理

- 证明：

由定义可知，`所有满足 两个端点均在选定点集中 的边都在导出子图中`。若导出子图不是弦图，则在变为原图的加边过程中，肯定不能添加到一条弦切开导出子图中 $\ge 4$ 的环。与题设矛盾，所以该导出子图一定为弦图。

--------

$\textbf{Lemma2:}$ 在弦图中，若 $u,v$ 存在割集，则 $u,v$ 的**极小**点割集的导出子图为团。

- 证明：


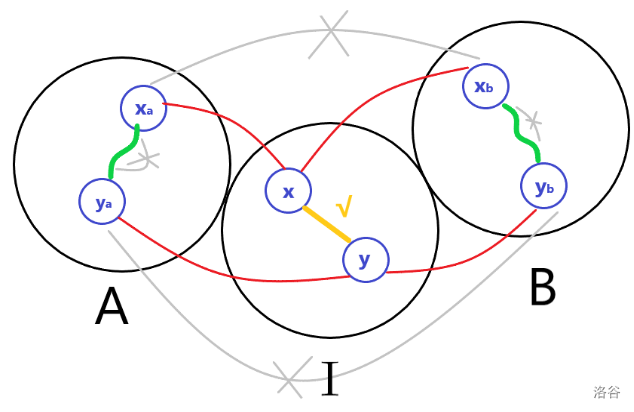
设 $u,v$ 的极小点割集为 $I$，删去 $i$ 后 $u,v$ 所在的连通块为 $A,B$。

若极小点割集点数 $=1$，显然是团。

若点数 $\ge 2$，设极小点割集上有两点 $x,y$，则 $x,y$ 一定与 $A,B$ 之间的点有边相连（否则 $I$ 删去 $x,y$ 后仍是点割集，不满足极小点割集定义）。设其相连的点分别为 $x_a,x_b,y_a,y_b$，则一定存在环 $\{x \rightarrow x_a \sim y_a \rightarrow y \rightarrow y_b \sim x_b \rightarrow x\}$，其中，$u \sim v$ 表示 $u$ 到 $v$ 的最短路（默认边权为 $1$）。显然该环的大小一定 $\ge 4$，所以环上肯定存在弦。

因为这条弦不能连接 $A,B$（否则 $I$ 不是点割集），不能在 $A$ 或 $B$ 内连接（否则 $x_{a/b} \sim y_{a/b}$ 不是最短路），所以该弦一定连接 $x,y$。

因此 $I$ 中任意两点 $x,y$ 都有边相连，证毕。

---------

$\textbf{Lemma3:}$ **非完全图**的弦图至少存在两个**不相邻**的单纯点。

- 证明：

考虑用归纳法证明。

假设现在已经证明了点数 $<|V|$ 的弦图满足引理。

对于点集为 $V$，边集为 $E$ 的弦图，若为完全图，显然满足引理；若不是完全图，则一定存在 $(u,v)$ 满足 $\{u\rightarrow v\}\notin E$，也就是 $u,v$ 之间一定存在点割集。设 $u,v$ 的极小点割集为 $I$，设删去 $I$ 后，$u$ 所在的连通块为 $A$。

由于 $A$ 是导出子图，根据 $\textbf{Lemma1}$ 可知，$A$ 是弦图。由 $\textbf{Lemma2}$ 可知，$I$ 是团，即弦图。所以图 $G=I+B$ 一定也是弦图，且点数 $<|V|$。所以 $G$ 满足引理。若 $G$ 是完全图，则每个点都是单纯点，$A$ 中一定含有单纯点；若 $G$ 不是完全图，由 $\textbf{Lemma2}$ 可知 $I$ 是团，只有一个不相邻的单纯点，所以 $A$ 中一定含有单纯点。

同理可得 $B$ 中也含有单纯点。又因为 $A,B$ 存在割集，所以 $A,B$ 中的单纯点不相邻，符合引理。

又因为当点数 $\ge 3$ 时符合引理（手膜一下就好），所以任何弦图都符合引理，证毕。

--------

$\textbf{Lemma4:}$ 一个无向图是弦图当且仅当其有完美消除序列。

- 证明：

若无向图是非弦图且存在完美消除序列，找到完美消除序列中最靠前出现的点 $v_i$，满足 $v_i$ 存在于一个 $\ge 4$ 且无弦的环上。设在环上与其相邻的点为 $v_j,v_k$，则 $v_j,v_k$ 在弦图中的位置位于 $v_i$ 后。根据完美消除序列的定义可得 $v_j,v_k$ 之间有边相连，与题设矛盾。所以非弦图没有完美消除序列（必要性）。

假设点数为 $(|V|-1)$ 的弦图有完美消除序列，对于点数为 $|V|$ 的弦图，删去一个单纯点（由 $\textbf{Lemma2}$ 可知，弦图存在消除点），由 $\textbf{Lemma1}$ 可知，剩下的导出子图为弦图，存在完美消除序列；再将删除的单纯点放到完美消除序列的开头即可（充分性）。

# 最大势算法（$\text{MCS}$ 算法）

一种线性求弦图完美消除序列的算法。

设 $label_x$ 表示点 $x$ 与多少已标号的点相邻，算法流程如下：

1. 将一个 $label$ 值最大的点标号，并插入完美消除序列的**开头**。

2. 更新点的 $label$ 值。

3. 重复 $1,2$ 步至所有点都被标号。

------

- 正确性证明：

设 $\gamma(x)$ 表示 $x$ 在最大势生成的序列中的位置。

证明一个序列是完美消除序列，等价于证明对于序列中的数 $u$，若 $u$ 与 $v,w$ 相连且 $\gamma(u)<\gamma(v)<\gamma(w)$，$v,w$ 一定有边相连（考虑前 $i$ 项满足完美消除序列特征，归纳法证明即可）。

 

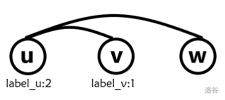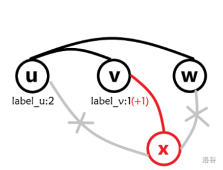
假设 $v$ 与 $w$ 没有边相连（如左图），为了保证 $\gamma(v)>\gamma(u)$，一定存在点 $x$ 满足 $\gamma(x)>\gamma(w)$，且 $x$ 与 $v$ 有边相连，与 $u$ 没有边相连。同样还有 $x$ 与 $w$ 没有边相连，否则会出现 $\{u\rightarrow v \rightarrow x \rightarrow w \rightarrow u\}$ 的环且环上无弦，与弦图定义矛盾（如右图）。

 

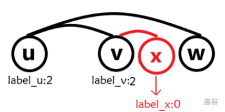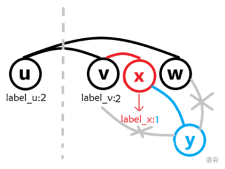
若 $\gamma(u)<\gamma(v)<\gamma(x)<\gamma(w)$（如左图），因为 $x,w$ 无边相连，$u,w$ 有边相连，为了保证 $\gamma(u)<\gamma(x)$，一定存在点 $y$ 满足 $\gamma(y)>\gamma(x)$，且 $y$ 与 $x$ 相连，与 $w$ 不相连（否则会存在 $\ge 4$ 的环，如右图）。

 

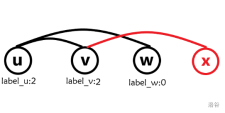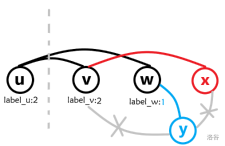
若 $\gamma(u)<\gamma(v)<\gamma(w)<\gamma(x)$（如左图），因为 $x,v$ 有边相连，$x,w$ 无边相连，为了保证 $\gamma(v)<\gamma(w)$，一定存在点 $y$ 满足 $\gamma(y)<\gamma(w)$ 且 $y$ 与 $w$ 相连，与 $v$ 不相连（否则会存在 $\ge 4$ 的环，如右图）。

可以发现，该结论会引入新节点 $y$，为了使 $y$ 满足完美序列特征，用上述方式继续分析，会不断引入新节点。最终肯定会出现矛盾。

---------

实现的话还有些细节。考虑开 $m$ 个双向链表 $v$，$v_x$ 存储 $label=x$ 的所有点。

步骤 $2$ 更新时，直接将更新后的点插入对应的 $v_x$ 中并更新 $\max\{label\}$，**不用删除**更新前的点。

步骤 $1$ 找点时，暴力从**当前更新**的 $\max\{label\}$ 开始找，不符合条件的从链表中删除（即步骤 $2$ 中未删除的更新前的点），找到第一个符合条件的点为止。注意，若 $v_{\max\{label\}}$ 中所有点都被删除了，$\max\{label\}$ 值减一。

```cpp

#include

using namespace std;

const int maxn=10010;

const int maxm=1000010;

inline int read(){

int x=0;

char c=getchar();

for(;!(c>='0'&&c<='9');c=getchar());

for(;c>='0'&&c<='9';c=getchar())

x=(x<<1)+(x<<3)+c-'0';

return x;

}

struct edge{

int v,to;

}e[maxm<<1];

int head[maxn],ecnt;

void addedge(int u,int v){

e[++ecnt].v=v,e[ecnt].to=head[u],head[u]=ecnt;

}

vectorv[maxm];

//用vector模拟链表

int rnk[maxn],id[maxn];

//rnk[x]:x在完美消除序列中的位置

//id[i]:完美消除序列第i位的值

int label[maxn];

int n,m,ans;

void MCS(){

bool flag=0;

int Maxl=0,x;

for(int i=1;i<=n;i++)

v[0].push_back(i);

for(int t=n;t;t--){

while(!flag){

while(!v[Maxl].empty())

if(rnk[*(v[Maxl].end()-1)]||label[*(v[Maxl].end()-1)]!=Maxl)

v[Maxl].pop_back();

//判断两种不合法的情况

//其实第二个判断没必要,想一想为什么

else if(label[*(v[Maxl].end()-1)]==Maxl){

x=(*(v[Maxl].end()-1)),flag=1;

v[Maxl].pop_back();

break;//选点

}

if(!flag) Maxl--;

//v_Maxl中不存在合法点

}

id[t]=x,rnk[x]=t,flag=0;

for(int i=head[x];i;i=e[i].to)

if(!rnk[e[i].v]){

v[++label[e[i].v]].push_back(e[i].v);

Maxl=max(Maxl,label[e[i].v]);

//插入点,更新Maxl

}

}

}

int main(){

int x,y;

n=read(),m=read();

for(int i=1;i<=m;i++){

x=read(),y=read();

addedge(x,y),addedge(y,x);

}

MCS();

return 0;

}

```

- 时间复杂度证明：

每条边最多会让一个点加入链表中，所以链表的插入和删除复杂度为 $O(m)$。

每次找点时，最劣情况为 $\max\{label\}$ 一直降到 $0$，所以最劣复杂度为 $O(\sum\max\{label\})$。由于每一个点只会对 $\max\{label\}$ 进行一次有效更新（在被标号时），所以 $O(\sum\max\{label\})=O(\sum label)$。又因为每条边只会对 $\sum label$ 贡献 $1$，所以 $O(\sum\max\{label\})=O(\sum label)=O(m)$。

因此总时间复杂度不高于 $O(n+m)$。

# 应用

弦图的精髓就是最大势算法。关于弦图的所有应用，基本上都是**通过最大势算法**求解。

- ## 弦图判定

例题：[**SP5446 FISHNET - Fishing Net**](https://www.luogu.com.cn/problem/SP5446)

由 $\textbf{Lemma4}$ 可知，非弦图是没有完美消除序列的，而通过最大势算法，我们一定可以得到一个 $1$ 到 $n$ 的排列，所以只需要判断该排列是否为完美消除序列即可。

暴力判定是 $O(nm)$ 的，考虑更高效的判定方法。

假设对于序列的后 $(n-i)$ 项 $\{v_{i+1},\dots,v_n\}$ 仍满足完美消除序列的特征，考虑判定 $\{v_i,v_{i+1},\dots,v_n\}$ 是否也满足完美消除序列特征。

设 $v_i$ 与 $\{v_{i+1},\dots,v_n\}$ 中**直接相连**的点为 $\{v_{c_1},v_{c_2},\dots,v_{c_k}\}(c_i

又因为 $v_{c_1}$ 满足完美消除序列特征，所以只要 $v_{c_1}$ 与剩余的点都相连，$V=\{v_{c_1},v_{c_2},\dots,v_{c_k}\}$ 的导出子图一定是完全图。

因此，对于每个点 $v_i$，只需要分别求出其对应的 $\{v_{c_1},v_{c_2},\dots,v_{c_k}\}$，然后判断 $v_{c_1}$ 是否与剩余点**直接相连**即可。

----

将每条边 $(u,v)$ 压成一个数存入哈希表，每次查询即可。时间复杂度 $O(m+n)$。

部分代码如下：

```cpp

struct Hash{

int u,v,to;

}H[maxm<<1];

int Head[p],hcnt;

void addhsh(int x,int u,int v){

H[++hcnt].u=u,H[hcnt].v=v,H[hcnt].to=Head[x],Head[x]=hcnt;

}

void Insert(int u,int v){

int x=(u*(n+1ll)+v)%p;

for(int i=Head[x];i;i=H[i].to)

if(H[i].u==u&&H[i].v==v) return ;

addhsh(x,u,v);

}

bool Be(int u,int v){

int x=(u*(n+1ll)+v)%p;

for(int i=Head[x];i;i=H[i].to)

if(H[i].u==u&&H[i].v==v) return 1;

return 0;

}

//以上是哈希表

int main(){

int x,y;

n=read(),m=read();

for(int i=1;i<=m;i++){

x=read(),y=read();

Insert(x,y),Insert(y,x);

addedge(x,y),addedge(y,x);

}

mcs();int cnt=0,flag=1;

for(int i=n;i&&flag;cnt=0,i--){

for(int j=head[id[i]];j;j=e[j].to)

//找到与id[i]相连且在序列后方的所有节点,存入tmp

if(rnk[e[j].v]>i){

tmp[++cnt]=e[j].v;

if(rnk[e[j].v]

swap(tmp[1],tmp[cnt]);

}

for(int j=2;j<=cnt;j++)

//哈希判断v_c1是否与v_cj相连

if(!Be(tmp[1],tmp[j])){

printf("Imperfect\n");

flag=0;break;

}

}

if(flag) printf("Perfect\n\n");

return 0;

}

```

- ## 弦图染色问题/最大团问题

例题：[**P3196 [HNOI2008]神奇的国度**](https://www.luogu.com.cn/problem/P3196)

设图 $G$ 的最小染色数为 $\chi(G)$，最大团为 $\omega(G)$，有结论 $\chi(G)=\omega(G)$。

- 证明：

由于完全图每个点的颜色都不一样，所以有 $\chi(G) \ge \omega(G)$。

考虑一种构造染色数的方法，即按照完美消除序列**倒序**染色。设构造出的染色数为 $C$。

首先一定有 $C \ge \chi(G)$。

当对点 $v_i$ 进行染色时，只有 $\{v_{c_1},v_{c_2},\dots,v_{c_k}\}$ 中的点才会对其颜色进行限制（$c$ 序列沿用 `弦图判定` 一节的定义）。由 `弦图判定` 一节可知，$\{v_i,v_{c_1},v_{c_2},\dots,v_{c_k}\}$ 是完全图，即两两颜色都不同，所以对于点 $v_i$ 来说，颜色数为 $(k+1)$。因此，$C=\max\{k+1\}=\omega(G)$。

从而有 $C=\omega(G) \ge \chi(G),C=\omega(G)\le \chi(G)$，得 $C=\omega(G)=\chi(G)$。

同时也得到了 $\chi(G),\omega(G)$ 的线性求解方法。

注意，如果只求染色数而不用求染色方案，则答案为 $\max\{label_x+1\}$（ $label_x$ 等价于在完美消除序列中，处于点 $x$ 后且与点 $x$ **直接相连**的点的个数）。

主要代码如下：

```cpp

int main(){

int x,y;

n=read(),m=read();

for(int i=1;i<=m;i++){

x=read(),y=read();

addedge(x,y),addedge(y,x);

}

MCS();

for(int i=1;i<=n;i++)

ans=max(ans,label[i]+1);

//求解答案，正确性已证明

printf("%d\n",ans);

return 0;

}

```

- ## 弦图最小团覆盖/最大独立集

设图 $G$ 的最小团覆盖数为 $\kappa(G)$，最大独立集为 $\alpha(G)$。

仍然有结论 $\kappa(G)=\alpha(G)$。

- 证明：

由于每个团中最多选一个点，所以有 $\alpha(G) \le \kappa(G)$。

考虑一种构造独立集的方法，即按照完美消除序列**顺序**求独立集。设选出的点数为 $T$。

首先肯定有 $T \le \alpha(G)$。每个点 $x$ 选完后，在 $x$ 后方且与 $x$ 有边相连的点都不能选，根据完美消除序列的定义，$x$ 支配了一个团。所以 $T$ 也是一个团覆盖数，有 $T \ge \kappa(G)$。

$\kappa(G)\le T \le \alpha(G),\kappa(G) \ge \alpha(G)$，结合两者得 $T=\kappa(G)=\alpha(G)$。

同时也得到了 $\alpha(G),\kappa(G)$ 的线性求解方法（每条边只遍历一次，显然线性）。

主要代码如下：

```cpp

int main(){

int x,y;

n=read(),m=read();

for(int i=1;i<=m;i++){

x=read(),y=read();

addedge(x,y),addedge(y,x);

}

MCS();int ans=0;

for(int i=1;i<=n;i++)

if(!vis[id[i]]){

ans++;

for(int j=head[id[i]];j;j=e[j].to)

vis[e[j].v]=1;

}

printf("%d\n",ans);

return 0;

}

```

另外，显然有最小点覆盖等于最小团覆盖。

- ## 区间图

区间图定义：有若干个区间，把每个区间当做一个点，两个点之间有连边当且仅当两个区间有交集。

以下是一个区间图的构造：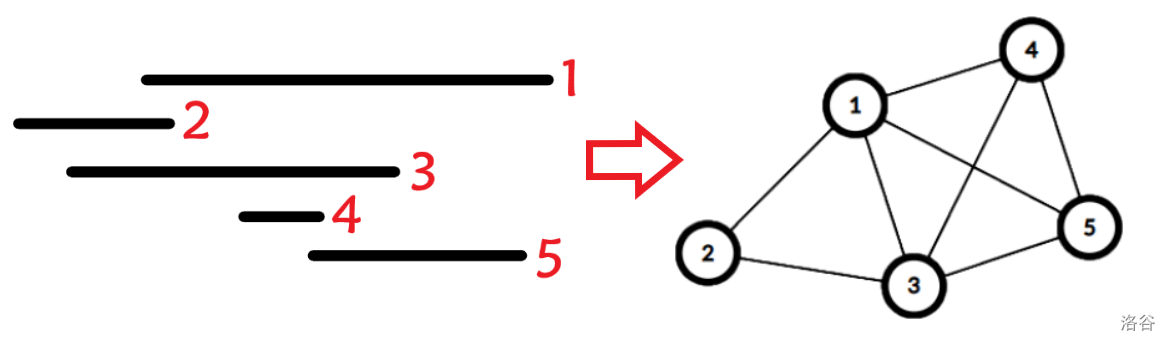


之所以提到区间图，是因为区间图有一个很好的性质——所有的区间图都是弦图。

- 证明：

首先，如果环长 $\le 3$，该环一定是团，可构造（可以看做环上每一条边都是弦）。

假设区间图存在无弦的环 $\{v_1,v_2,\dots,v_k\}$，由于无弦，$v_i,v_{i+1}$ 两两交集位置一定**严格**单调递增或递减（可以手膜一下，如果不单调一定有弦），则 $v_1,v_k$ 的交集一定为空，矛盾。

-----------

对于区间问题，可以先构造区间图，再根据弦图的性质求解。

（不过有一说一这个用处不大，毕竟区间图还有很多更优的性质qwq）